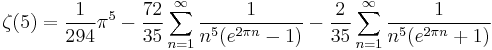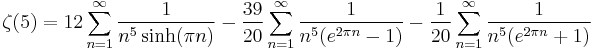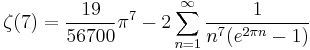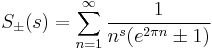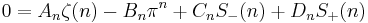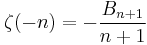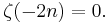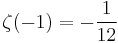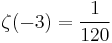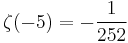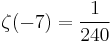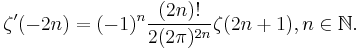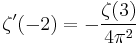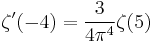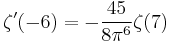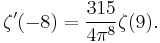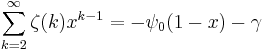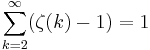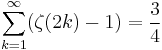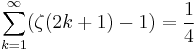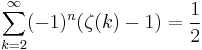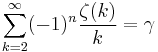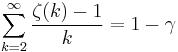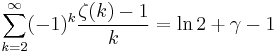Zeta constant
In mathematics, a zeta constant is a number obtained by plugging an integer into the Riemann zeta function. This article provides a number of series identities for the zeta function for integer values.
Contents |
The Riemann zeta function at 0 and 1
At zero, one has
There is a pole at 1, so 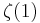 is not defined but the left and right limits are:
is not defined but the left and right limits are:
and 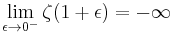
Positive integers
Even positive integers
For the even positive integers, one has the well-known relationship to the Bernoulli numbers, given by Euler:
for 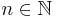 . The first few values are given by:
. The first few values are given by:
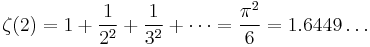 ( A013661)
( A013661)- (the demonstration of this equality is known as the Basel problem)
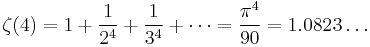 ( A013662)
( A013662)- (the Stefan–Boltzmann law and Wien approximation in physics)
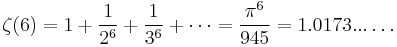 ( A013664)
( A013664)
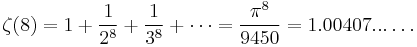 ( A013666)
( A013666)
 ( A013668)
( A013668)
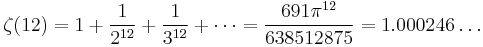 ( A013670)
( A013670)
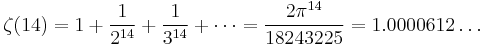 ( A013672)
( A013672)
The relationship between zeta at the positive even integers and the Bernoulli numbers may be written as
where An and Bn are integers for all even n. These are given by the integer sequences A046988 and A002432 in OEIS. Some of these values are reproduced below:
| 2n | A | B |
|---|---|---|
| 2 | 6 | 1 |
| 4 | 90 | 1 |
| 6 | 945 | 1 |
| 8 | 9450 | 1 |
| 10 | 93555 | 1 |
| 12 | 638512875 | 691 |
| 14 | 18243225 | 2 |
| 16 | 325641566250 | 3617 |
| 18 | 38979295480125 | 43867 |
| 20 | 1531329465290625 | 174611 |
| 22 | 13447856940643125 | 155366 |
| 24 | 201919571963756521875 | 236364091 |
| 26 | 11094481976030578125 | 1315862 |
| 28 | 564653660170076273671875 | 6785560294 |
| 30 | 5660878804669082674070015625 | 6892673020804 |
| 32 | 62490220571022341207266406250 | 7709321041217 |
| 34 | 12130454581433748587292890625 | 151628697551 |
If we let 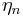 be the coefficient
be the coefficient 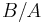 as above,
as above,
then we find recursively,
This recurrence relation may be derived from that for the Bernoulli numbers.
The even zeta constants have the generating function:
Since 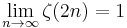 , the formula also shows that for
, the formula also shows that for 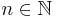 :
:
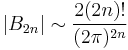 as
as 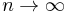
where the symbol ~ means "asymptotic to" (see asymptotic notation).
Odd positive integers
For the first few odd natural numbers one has
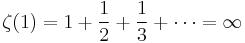 (the harmonic series);
(the harmonic series);
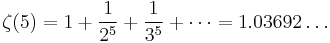 A013663
A013663
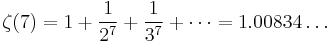 A013665
A013665
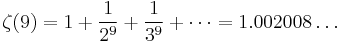 A013667
A013667
It is known that ζ(3) is irrational (Apéry's theorem) and that infinitely many of the numbers ζ(2n+1) (n ∈ N) are irrational. There are also results on the (ir)rationality of values of the Riemann zeta function at the elements of certain subsets of the positive odd integers; for example, at least one of ζ(5), ζ(7), ζ(9), or ζ(11) is irrational. This has significance for application to physics. Correlation functions in antiferromagnetic xxx spin chain can be expressed in terms of values of zeta at odd argumets 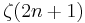 .
.
Most of the identities following below are provided by Simon Plouffe. They are notable in that they converge quite rapidly, giving almost three digits of precision per iteration, and are thus useful for high-precision calculations.
ζ(5)
Plouffe gives the identities
and
ζ(7)
Note that the sum is in the form of the Lambert series.
ζ(2n+1)
By defining the quantities
a series of relationships can be given in the form
where 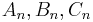 and
and 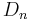 are positive integers. Plouffe gives a table of values:
are positive integers. Plouffe gives a table of values:
| n | A | B | C | D |
|---|---|---|---|---|
| 3 | 180 | 7 | 360 | 0 |
| 5 | 1470 | 5 | 3024 | 84 |
| 7 | 56700 | 19 | 113400 | 0 |
| 9 | 18523890 | 625 | 37122624 | 74844 |
| 11 | 425675250 | 1453 | 851350500 | 0 |
| 13 | 257432175 | 89 | 514926720 | 62370 |
| 15 | 390769879500 | 13687 | 781539759000 | 0 |
| 17 | 1904417007743250 | 6758333 | 3808863131673600 | 29116187100 |
| 19 | 21438612514068750 | 7708537 | 42877225028137500 | 0 |
| 21 | 1881063815762259253125 | 68529640373 | 3762129424572110592000 | 1793047592085750 |
These integer constants may be expressed as sums over Bernoulli numbers, as given in (Vepstas, 2006) below.
The only fast algorithm for calculation of Riemann's zeta function for any integer argument was found by E.A. Karatsuba[1][2][3]
Negative integers
In general, for negative integers, one has
for 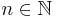 .
.
The so-called "trivial zeros" occur at the negative even integers:
The first few values for negative odd integers are
However, just like the Bernoulli numbers, these do not stay small for increasingly negative odd values. For details on the first value, see 1 + 2 + 3 + 4 + · · ·.
Derivatives
The derivative of the zeta function at the negative even integers is given by
The first few values of which are
One also has
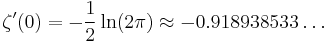 A075700
A075700
and
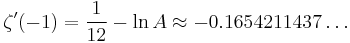 A084448
A084448
where  is the Glaisher-Kinkelin constant.
is the Glaisher-Kinkelin constant.
Sum of zeta constants
The following sums can be derived from the generating function:
where 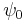 is the digamma function.
is the digamma function.
Series related to the Euler–Mascheroni constant (denoted by γ) are
References
- ^ E.A. Karatsuba: Fast computation of the Riemann zeta-function ζ(s) for integer values of the argument s. Probl. Inf. Transm. Vol.31, No.4, pp.353-362 (1995).
- ^ E.A. Karatsuba: Fast computation of the Riemann zeta function for integer argument. Dokl. Math. Vol.54, No.1, p.626 (1996).
- ^ E.A. Karatsuba: Fast evaluation of ζ(3). Probl. Inf. Transm. Vol.29, No.1, pp.58-62 (1993).
- Simon Plouffe, "Identities inspired from Ramanujan Notebooks", (1998).
- Simon Plouffe, "Identities inspired by Ramanujan Notebooks part 2 PDF" (2006).
- Vepstas, Linas (2006). "On Plouffe's Ramanujan Identities". arXiv:math.NT/0609775.
- Zudilin, Wadim (2001). "One of the Numbers ζ(5), ζ(7), ζ(9), ζ(11) Is Irrational". Russian Math Surveys 56: 149–150. doi:10.1070/RM2001v056n04ABEH000427. MR1861452. PDF PDF Russian PS Russian
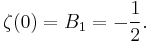
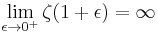
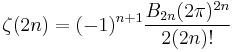
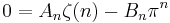
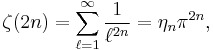
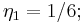
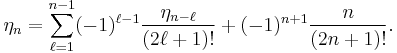
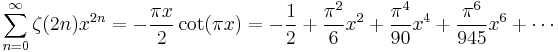
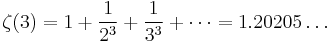 (
(